by Nathan Day (@nathanday314)
In today’s Year 8 lesson I discovered a startling fact: the number of cuboids you can make from 𝑛 cubes is equal to the number of non-prime factors of 𝑛.
Not long later, I discovered an even startlinger fact: this isn’t true. At least, not for all 𝑛.
I decided this would make for an interesting investigation, interweaving ideas about volume, factors, primes and systematic counting.
I would suggest starting with the questions:
Pupils can then find the same two properties of different numbers, at first aimlessly, later with the goal of finding numbers that give 1 cuboid, 2 cuboids, 3 cuboids etc.
Pupils will find that the two quantities are always equal (unless they are unlucky with their choices), and will be able to generalise to some nice results, e.g.
However, the two quantities are not always equal! [Spoilers below images.]
Below is my summary of the two key properties, and some prompts for guiding the investigation.
This can be given as much or as little structure as you feel appropriate.
 Summary
Summary
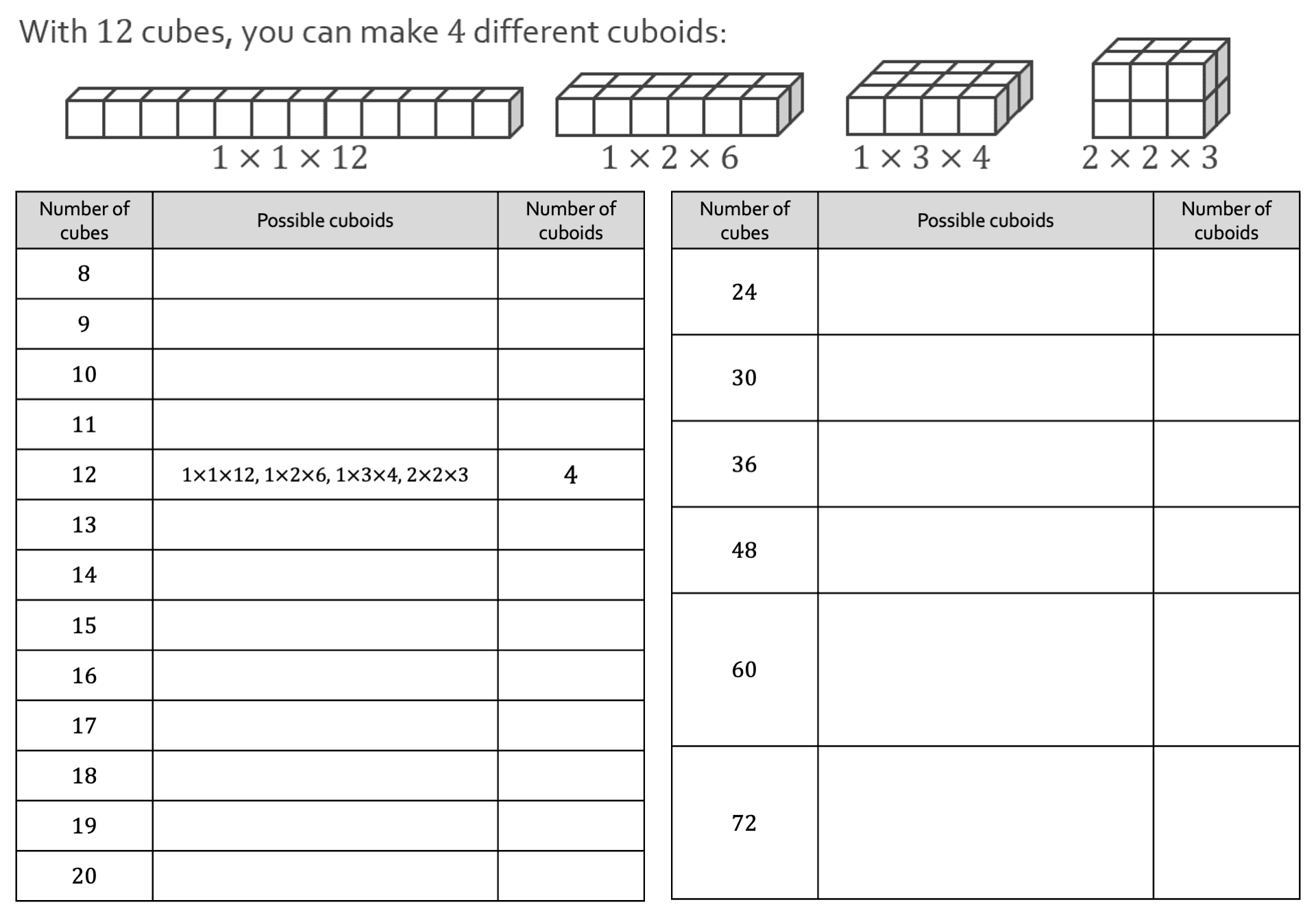
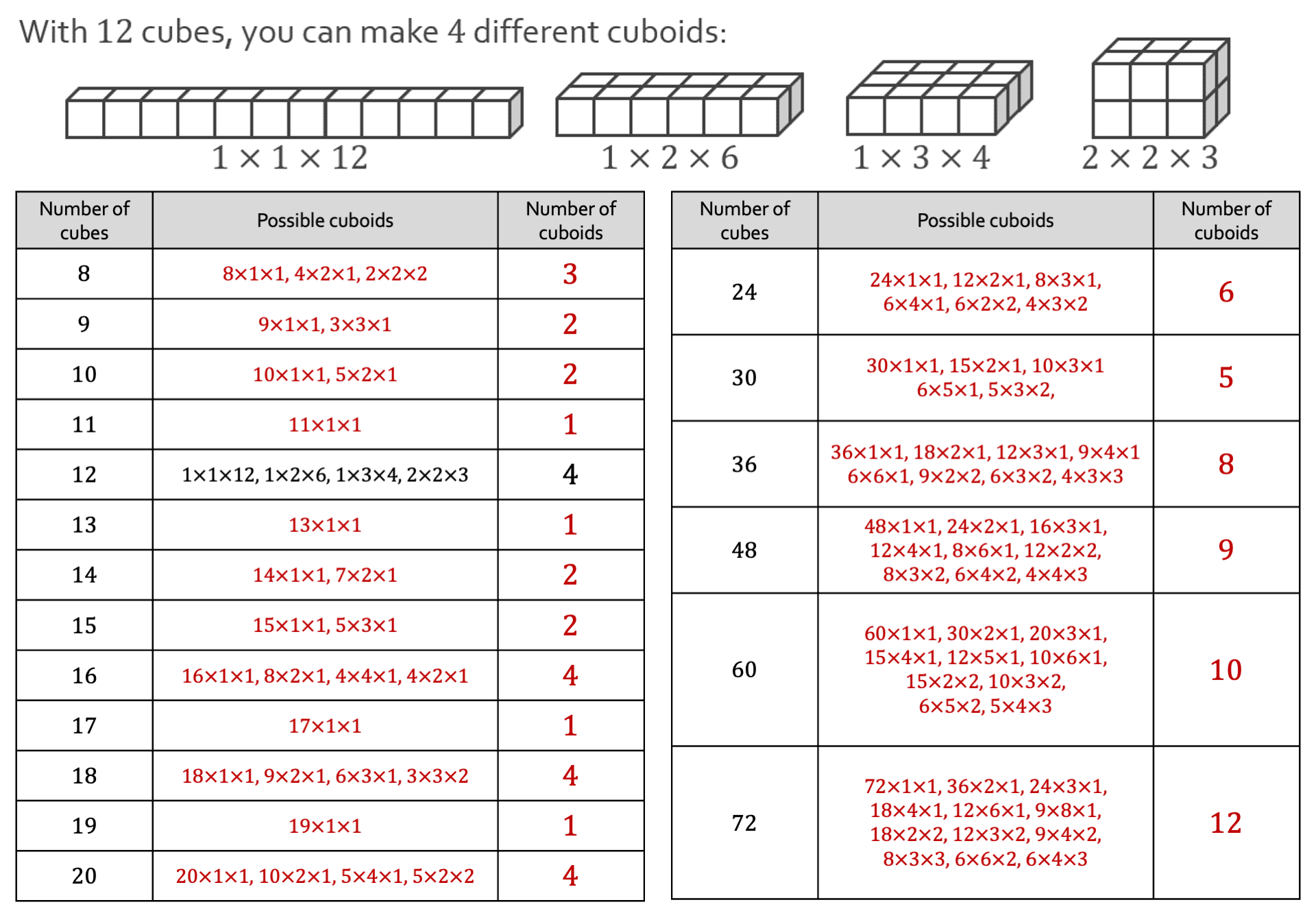

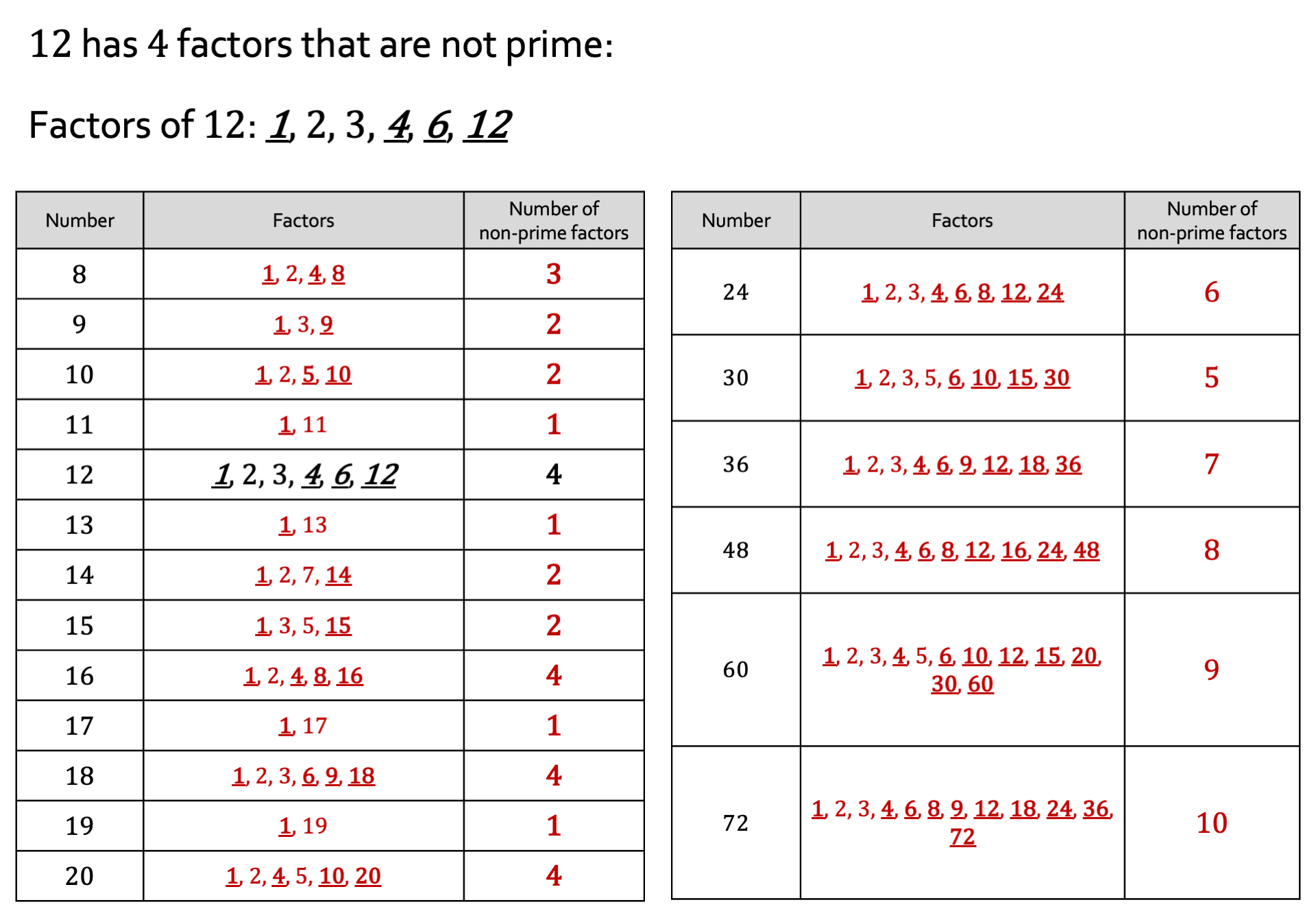
[They aren’t equal for 𝑛 = 36, 48, 60, 64,..]